This unindicted five-year-old checks the record

WAGS @ UC Riverside, 5-6 November 2022 – IN PERSON

The Fall 2022 edition of the Western Algebraic Geometry Symposium (WAGS) will be held at UC Riverside on the weekend of 5-6 November 2022.

Speakers confirmed so far are:
Olivia Dumitrescu (UNC Chapel Hill),
James McKernan (UC San Diego),
Joaquín Moraga (UCLA),
Jenia Tevelev (UMass Amherst),
Chengxi Wang (UCLA),
Rachel Webb (UC Berkeley), and
Tony Yue Yu (Caltech).

Registration is free and is open now until 15 October. There will be a poster session on Saturday. Funding for participants is available.

Details from the organizers:
“We are pleased to inform you that the conference can offer a minimum of $400 for the first 80 attendants requiring funding. We will have the registration form open until October 15, so we can coordinate the banquet, coffee, snacks, etc. The allocation of this funding will prioritize students and will likely be adjusted depending on the geographical situation of each participant.

“We are aware this might not cover all the expenses, and we hope we are able to provide more funding to all of you who request it, however, without the full registration list and other information it’s impossible to give exact numbers. We appreciate your understanding.

“We also strongly encourage you to use the discord to coordinate lodging and transportation with other attendants and share some expenses. You can join it at: https://discord.gg/YZkM2YmcVM “

WAGS @ Colorado State, 22–24 April 2022, IN PERSON

Oreo (2004–2020), the Armstrong Hotel cat. Photo by Austin Humphreys/The Coloradoan

The Spring 2022 edition of the Western Algebraic Geometry Symposium (WAGS) will take place Friday 22 April to Sunday 24 April at Colorado State University. Register for free at the conference website.

The speakers are Jordan Ellenberg, Sarah Frei, Patricio Gallardo, Tyler Kelly, Burt Totaro, Ravi Vakil, and Cynthia Vinzant, several of whom will also contribute to an event for undergraduates.

I look forward to seeing you all there!

This skeptical four-year-old is waiting to be convinced

New paper: Varieties of general type with many vanishing plurigenera, and optimal sign and sawtooth inequalities

Louis Esser, Terry Tao, Chengxi Wang and I posted a new paper on the arXiv. As the list of authors might suggest, the paper uses a surprising combination of techniques.

We construct smooth projective varieties of general type with the smallest known volumes in high dimensions. These are n-folds with volume roughly 1/e^n3/2. Among other examples, we construct varieties of general type with many vanishing plurigenera, more than any polynomial function of the dimension.

The examples are resolutions of singularities of general hypersurfaces of degree d with canonical singularities in a weighted projective space P(a₀,…,a_n+1). The volume can be calculated explicitly in terms of the weights a_i, and so the problem is to make a good choice of these numbers. In the class of examples we consider, we minimize the volume by reducing to a purely analytic problem about equidistribution on the unit circle.

Namely, consider the sawtooth (or signed fractional part) function, the periodic function on the real line which is the identity on the interval (-1/2,1/2]. For each positive integer m and every probability measure on the real line, at least one of the dilated sawtooth functions g(kx) for k from 1 to m must have small expected value, and we determine the optimal bound in terms of m. We also solve exactly the corresponding optimization problem for the sine function.

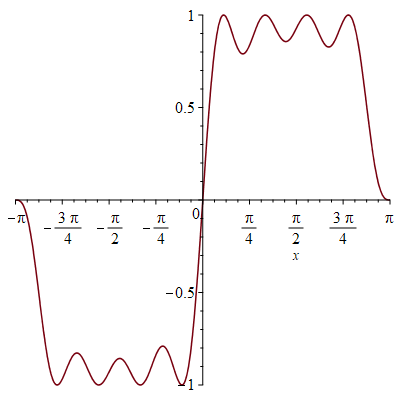
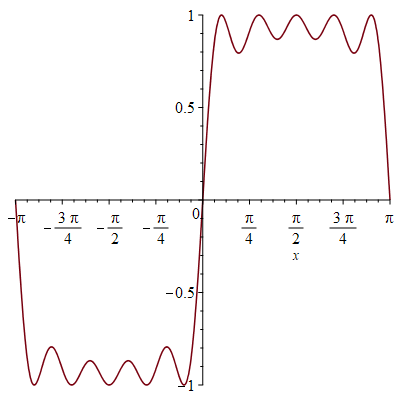
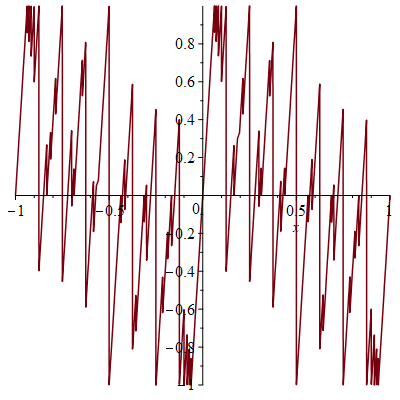
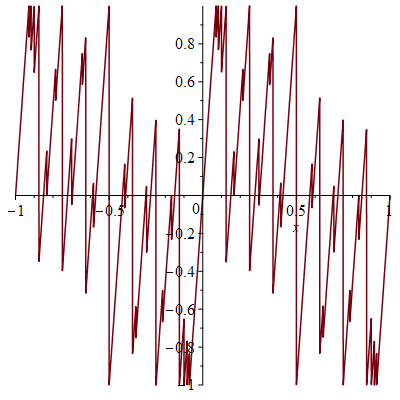
Equivalently, we find the optimal inequality of the form ∑_k=1^m a_k sin kx≤ 1 for each positive integer m, in the sense that ∑_k=1^m a_m is maximal. The figures show examples of these inequalities, which show striking cancellation among dilated sine or sawtooth functions.

New paper: Varieties of general type with small volume

Chengxi Wang and I posted a new paper on the arXiv.

By Hacon-McKernan, Takayama, and Tsuji, there is a constant r_n such that for every r at least r_n, the r-canonical map of every n-dimensional variety of general type is birational. We give examples to show that r_n must grow faster than any polynomial in n.

Related to this, we exhibit varieties of several types (Fano, Calabi-Yau, or general type) with small volume in high dimensions. In particular, we construct a mildly singular (klt) n-fold with ample canonical class whose volume is less than 1/2^(2^n). The klt examples should be close to optimal.

All our examples come from weighted projective hypersurfaces. These exhibit a huge range of behavior, and it is not at all clear how to find the best weighted hypersurfaces for these problems. It’s an attractive problem to explore in combinatorial number theory.

For example, Gavin Brown and Alexander Kasprzyk’s computer program shows that the smallest volume for a weighted hypersurface of dimension 2 which is quasi-smooth (hence klt) and has ample canonical class is 2/57035, about 3.5 x 10^{-5}. This occurs for a general hypersurface of degree 316 in the weighted projective space P(158,85,61,11). What is the pattern behind these numbers? Chengxi Wang and I found one pattern and used it to produce examples with small volume in all dimensions. But one can try to do better.

Image: Maru attempting to minimize his volume.

WAGS Virtual, 23–24 April 2021

The Spring 2021 edition of the Western Algebraic Geometry Symposium (WAGS) will take place virtually on 23–24 April 2021. There will be stimulating talks (short and long), a lively panel, informal office hours with established mathematicians, and social events.

For detailed information, and to register, visit the conference website.

Interested participants (regardless of career stage) can also submit information for virtual introductions that will play as a slideshow during the conference.

Image lifted from @JulietteBruce12.

This weary three-year-old has seen it all. (Go Bruins!)

WAGS @ Pomona, 13–14 November 2020

The Fall 2020 edition of the Western Algebraic Geometry Symposium (WAGS) will be held on November 13-14, 2020, via Zoom. You can register here. Pomona College is serving as host. The meeting will include an online poster session; please register by November 6 if you would like to present a poster.

Image: Bookstore cat who works at Magic Door Bookstore IV in downtown Pomona.

Morse theory on singular spaces

Morse theory is a powerful tool in topology, relating the global properties of a smooth manifold X to the critical points of a smooth function on X. In this note I want to consider the possibility of Morse theory on singular spaces. Some of this dream can be made to work in algebraic geometry, where it helps to analyze the Hilbert scheme of points in new cases.

This is related to my joint work with Marc Hoyois, Joachim Jelisiejew, Denis Nardin, Maria Yakerson on “The Hilbert scheme of infinite affine space.” The connection with Morse theory appears in my paper Torus actions, Morse homology, and the Hilbert scheme of points on affine space.

Morse theory studies a smooth function f on a closed Riemannian manifold X using the gradient flow associated to f. That is, from any point on X, move in the direction in which f is (say) decreasing fastest. In the limit, every point of X is attracted to one of the critical points of f.

From the modern point of view known as “Morse homology,” a central part of the theory is to compactify the space of orbits of the gradient flow. The key point is that any limit of orbits of the gradient flow is a broken trajectory, a chain of orbits that connect a sequence of critical points with decreasing values of f.

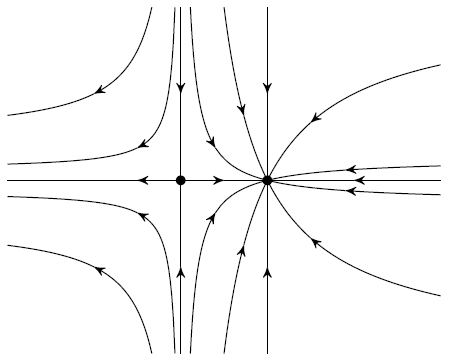
This situation has an analog in algebraic geometry. Consider a projective variety X with an action of the multiplicative group T = G_m. (Over the complex numbers, this group can also be called C^*.) Then the orbits of T on X are analogous to the gradient flow lines in Morse theory. In particular, for every point x in X, the “downward limit” of its orbit, lim_t→0(tx), is a T-fixed point of X (analogous to a critical point in Morse theory). Over the complex numbers, this T-action can actually be identified with Morse theory for the “Hamiltonian function” on X.

Just as in Morse theory, I show that every limit of T-orbits on a projective variety X is a broken trajectory, a chain of orbits that connect a sequence of T-fixed points. An interesting point is that this works without assuming that X is smooth. So this is a possible model for Morse theory on singular spaces.

I give an application to the Hilbert scheme of points on affine space. Namely, let Hilb_d(Aⁿ) be the space of 0-dimensional subschemes of degree d in affine n-space. And let Hilb_d(Aⁿ,0) be the (compact) subspace of subschemes supported at the origin in Aⁿ. I show that, over the complex numbers, these two spaces are homotopy equivalent. (Computing the cohomology of either space is a wide open problem, in general.) The proof uses the algebraic version of Morse theory described here, using the action of T on Hilb_d(Aⁿ) coming from the action on Aⁿ by scaling. I hope to see more applications: torus actions are everywhere in algebraic geometry.

Image: A chubby Tom Kitten in a broken pair of pants, from The Tale of Tom Kitten, by Beatrix Potter.